开端：公众号“算法与数学之好意思”东京热qvod

东谈主类的历史不错看作念一部对于平静的历史。也有这么的说法，懒惰是东谈主类向上的能源。为了偷懒，东谈主类连接的作念着各式奋发，发明了各式机器器具，将我方从极重的做事平静出来，另一方面，每一次大的向上，王人需要平静想想，同期也带来了全东谈主类想想的大平静。在这么的历程中，筹画机的出现无疑将东谈主类从许多极重的功课中平静了出来。与此同期，有些东谈主运行想考能否制造出不错像东谈主类一样进行想考的机器，以将东谈主类从创造性的做事和逻辑想收用平静出来，交给机器去完成。

自然筹画机的出现，不到百年，关联词为了它的出现，所进行的探索和研究，早已阅历经数百年的历史。自然准确的说，这些探索和研究在那时本质并不是为了筹画机产生而进行的，绝大精深只是作念了一个不测的铺垫。有时咱们并不闇练这么的一个历程，浑朴说当代的大学老师中也很少说起筹画机出现之前的那些历史。本质上，了解这么的一个历程，更有助于咱们交融一个事物是如何产生出来，它背后的科学旨趣又是如何，让咱们不错透过复杂的电路外在，战斗到最实质的东西。不错让咱们除了对科学家们的责任暗示颂扬以外，也不错真切他们当初的想想历程，近距离地进行跨越时候和空间的相易。这对于咱们我方应该如何想考问题，创造性地提议我方的想法亦然有所匡助的。

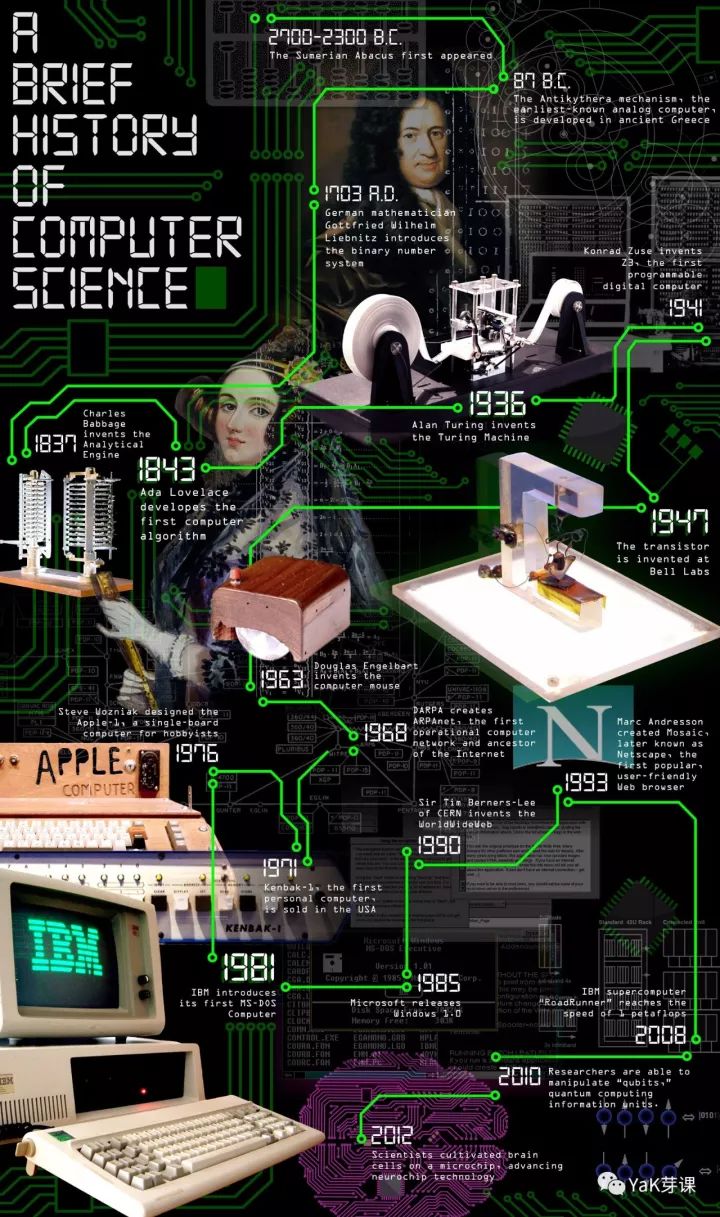
咱们还是了解到这么的一些东谈主物，乔治.布尔，康托，哥德尔，图灵，冯诺依曼。而咱们的疏忽数学的素质中，自身太戒备于学问自身的学习，而忽略了学问是如何被发现产生出来，以及不同的学问之间也曾的渊源和启发关系。而对于启迪想想来说，后者彰着更为有劲。

莱布尼茨之梦

早在17世纪的莱布尼茨就有一个伟大的构想，他但愿不错将东谈主类的想维像代数运算那样符号化，轨则化，从而让笨的东谈主通过掌持这么的轨则变得灵敏，更进一步的制造出不错进行想维运算的机器，将东谈主类从想收用平静。从莱布尼茨为微积分所详情的依然在今天被沿用的符号中，咱们不错看出他对符号具有简约的嗅觉，通过弃取简约的符号，不错大大的简化运算的复杂性，以致将这么的运算形成一种自然的历程。除了构想以外，莱布尼茨自身为了发展一种逻辑演算也进行了许多尝试，他得到的一些成果还是具有其后布尔的逻辑代数的雏形。

布尔的逻辑代数

19世纪的布尔，将逻辑代数化，发展出了逻辑代数成为其后筹画机里面运算的逻辑基础。

在早期的研究中，布尔就还是意志到符号的力量，代数的力量正源于代表着量和运算的符号在几条基本轨则的驾御下体现出来的。其后，他运行想考能否将逻辑推理也像代数那样用符号和几条基本轨则就不错完竣抒发。

他运行想考咱们常常所说的某物具有某种性质，不错用一个类来暗示，比如白的是x，绵羊是y，那么白绵羊就不错用xy来暗示，这么日常活命中的主见运行具有代数的神志，用当代的术语来说上头的xy暗示的恰是错乱。

他又连接想考，xx暗示什么呢，他发现xx与咱们粗鄙的代数运算不同xx依然暗示的是x。xx=x本质上成为布尔的逻辑代数的一个基本轨则。

连接筹商下去，若是xx=x在粗鄙的代数心仪味着什么呢？xx=x，意味着x=1或者0.不错看到若是xx=x作为逻辑代数的基本轨则，放在粗鄙代数心仪味着x=0或者1，那么逻辑代数是否意味着是01的粗鄙代数呢。于是布尔得到一个基答应趣，若是只是限于01，逻辑代数就形成了粗鄙代数。对于这极少的想考，对于二进制运算的在逻辑代数中的主导作用具有很大的启发谈理谈理。

若是限于01，那么01在咱们的逻辑代数中代表的谈理又是什么呢。咱们之前看到不错用x暗示某个类，对应地那么0不错解释成莫得任何东西属于它的类，1不错解释成包含扫数对象的全体。同期布尔又运行筹商粗鄙代数中的+-在逻辑代数中的谈理谈理，x+y不错暗示具有x和y两种属性的对象团结，x-y暗示具有x属性同期不具有y属性的对象团结。

拳交小说

筹商了这么的一些谈理谈理之后，接下来再看xx=x=> x-xx = 0 => x(1-x) = 0

当今咱们以逻辑代数的不雅点看这个式子，它体现了这么一个含义：莫得任何东西不错同期属于又不属于某个类。这点让布尔十分奋斗，因为这刚好体现了亚里士多德的排中律，这就使他坚信我方找对了门道。

连接下去，布尔发现三段论也不错用他的逻辑代数来抒发。

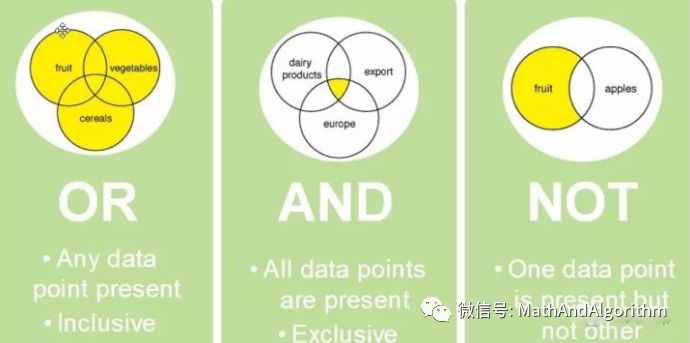
扫数x王人是y x=xy(x中的任何东西也属于y，就等于说莫得任何东西是属于x而不属于y的，也就是说x(1-y)=0)

扫数y王人是z y=yz

------------ ?

扫数x王人是z x=xz

x=xy

y=yz => x = xy = x(yz) = (xy)z = xz

终末，"若是x，那么y。"不错用x(1-y)=0来暗示，不错这么交融这个式子意味着若是x=1，那么y=1。在这里一方面咱们不错把"若是x，那么"交融为等同于前边的这么一句话"扫数的x王人是y"，自然这两者有一个区别，当今的x，y暗示的是命题，而正本的x，y暗示的则是类主见。以今天的不雅点来看，前者是命题演算，后者是谓词演算。

可是若是从另一个方面，再行筹商这句话，比如x=1暗示命题x为真，x=0暗示命题x为假，xy=1暗示x且y，独一x，y均为1，xy=1，若是x=0或y=0，xy=0，这点又与粗鄙代数相一致。从这个标的想考下去，就不错看到今天的布尔代数的基本面庞了，上头的这个界说恰是与运算。

布尔的逻辑体系，不仅包含了亚里士多德的逻辑体系，而且还杰出了它，可是仍有无法抒发的情形：扫数失败的学生或者是朦拢的或者是懒惰的。

今天的布尔代数

回到今天，咱们再看布尔再把逻辑转形成代数的历程中，所产生的逻辑代数在今天的筹画机中演出着什么样的作用。布尔代数独一1和0两个元素，not and or三种运算，用几张真值表就不错抒发明晰。

AND | 1 0东京热qvod

-----------------------

1 | 1 0

0 | 0 0

这张表阐发若是 AND 运算的两个元素有一个是 0，则运算成果老是 0。若是两个元素王人是 1，运算成果是 1。举例，“太阳从西边升空”这个判断是假的(0)，“水不错流动”这个判断是确实（1），那么，“太阳从西边升空况且水不错流动”就是假的（0）。

OR | 1 0

-----------------------

1 | 1 1

0 | 1 0

这张表阐发若是OR运算的两个元素有一个是 1，则运算成果老是 1。若是两个元素王人是 0，运算成果是 0。比如说，“张三是比赛第别称”这个论断是假的（0），“李四是比赛第别称”是确实（1），那么“张三或者李四是第别称”就是确实（1）。

NOT |

--------------

1 | 0

0 | 1

这张表阐发 NOT 运算把 1 形成 0，把 0 形成 1。比如，若是“象牙是白的”是确实（1），那么“象牙不是白的”必定是假的（0）。

如斯浅薄的运算，本质上那时的布尔也不会料想它会被哄骗到筹画机中，直到1938 年香农在他的硕士论文中指出用布尔代数来杀青开关电路，使得布尔代数成为数字电路的基础。扫数的数学和逻辑运算，加、减、乘、除、乘方、开方等等，沿路能颐养成二值的布尔运算。

用筹画的力量更变宇宙是每一个轨范员的渴望，YaK团队抱着对老师的敬仰和热忱，征战了谈理的YaK编程器具以及配套的系统化素质课程。让孩子不错用编程去学习和交融天主的谈话：数学。

媒介：东谈主类的历史不错看作念一部对于平静的历史。也有这么的说法，懒惰是东谈主类向上的能源。为了偷懒，东谈主类连接的作念着各式奋发，发明了各式机器器具，将我方从极重的做事平静出来，另一方面，每一次大的向上，王人需要平静想想，同期也带来了全东谈主类想想的大平静。在这么的历程中，筹画机的出现无疑将东谈主类从许多极重的功课中平静了出来。与此同期，有些东谈主运行想考能否制造出不错像东谈主类一样进行想考的机器，以将东谈主类从创造性的做事和逻辑想收用平静出来，交给机器去完成。

前边咱们看到筹画发源的数学想想有莱布尼茨，布尔代数。接下来咱们看到其他的数学想想在筹画中的哄骗。

弗雷格的打破与消沉

弗雷格的一世主要发表了这么三本文章：《主见演算--一种师法算术谈话构造的纯想维的符号谈话》（1879）、《算术的基础--对数主见的逻辑数学研究》（1884）《算术的基本礼貌》（l卷 1893，2卷1903）。

其中主见演算，将粗鄙数学中的一切演绎推理王人包含在内，成为第一个完备的逻辑体系。布尔以粗鄙代数为基础，用代数符号来暗示逻辑关系。与此相悖，弗雷格想以他的逻辑为基础而把代数构造出来。本质上这成为日后一个紧迫的流派"逻辑宗旨"，在他们看来逻辑与数学的关系就像一门学科的基本部分和高级部分之间的关系。

弗雷格的逻辑体系，表当今今天就是咱们数理逻辑中的命题演算和谓词演算(用数学的步伐研究对于推理、诠释等问题的学科就叫作念数理逻辑。也叫作念符号逻辑)。弗雷格第一次用精准的句法构造出神志化的东谈主工谈话，使得逻辑推理暗示为机械演算即所谓的推理轨则成为可能。从这个不雅点看，主见笔墨是咱们今天神用的筹画机轨范预备谈话的前身。

弗雷格但愿不错自然数提议一种金兰之友逻辑的表面，从而诠释算术，微积分乃至一切数学王人不错手脚逻辑的一个分支。于是弗雷格便但愿不错用纯逻辑的术语来界说自然数，然后再用他的逻辑导出它们的性质。举例3这个数将被解释为逻辑的一部分。弗雷格的想想是把3界说为扫数元素数为3的团结的团结。本质上这就是《算术的基础--对数主见的逻辑数学研究》这部文章的主要内容。

关联词恰是这么的一些责任，1902年，年青的伯特兰.罗素据此提议阿谁驰名的罗素悖论。弗雷格的算术使用了团结的团结这么一种主见。罗素指出，用团结的团结进行推理很容易导致矛盾。罗素的悖论不错这么态状：若是一个团结是它自身的一个成员，那么就把团结成为颠倒的，不然它就是泛泛的。那么由扫数泛泛团结组成的团结是泛泛照旧颠倒的呢？

若是是泛泛的，那么它应该包含自身，这么它就应该是颠倒的。若是是颠倒的，那么它就不会包含自身，这么它就应该是泛泛的。不管哪个成果王人导致了矛盾。本质上罗素构造这个悖论的步伐，与之后哥德尔，图灵构造不可判定命题却有着酷似的所在。关联词这一矛盾却标明弗雷格构造的算术体系所基于的那些前提是靠不住的，并给弗雷格带来了宏大的打击。

自然弗雷格的逻辑还是很完备，但仍然具有一些局限性。他的轨则并莫得提供判定某个论断能否从给定的前提中推导出来的筹画风光。另外能否找到一种筹画步伐，它能够阐发在弗雷格的逻辑中某一推理是正确的呢？其成果是这么一则诠释：莫得这么的一般步伐存在。关联词恰是在诠释这么一条含糊性的论断历程中，阿兰图灵发现原则上不错预备出一种通用机，它不错扩充当何可能的筹画。

弗雷格的研究开启谈话形而上学的大门，其后东谈主们在寻找诠释逻辑推理正确性的历程中，图灵发现了通用机，也就是今天筹画机的数学模子。

康托尔，对无尽的探索

康托尔参加无尽的宇宙，运行无尽的数方针研究。他发现自然数与实数具有不同的基数，以及由此提议的相连统假设，即实数和自然数之间不存在具有其他基数的团结。这亦然1900年，希尔伯特提议的23个问题中的第一问题。这个问题直到今天并未完竣惩处，1938年哥德尔和1963年保罗科恩的首要发现标明，若是相连统假设问题不错被惩处，就必须杰出粗鄙数学的步伐。

对于咱们粗鄙东谈主来说，最有用的或者是康托尔在诠释实数与自然数基数不同的历程中所采用的对角线步伐，这种步伐是1891年，康托尔在一篇4页的论文中发表的。而对角线步伐，在以后的故事中仍然会被用到，它将会被哥德尔用来惩处一致性问题时构造系统内不可证命题，然后阿兰.图灵又再次使用了哥德尔的步伐构造出了不可判定命题。而对于相连统假设的研究也激励了对于图灵机的构想。当今咱们不错看到康托尔的责任与筹画机的发源在这里产生了臆想。

对于对角线步伐，咱们从自然数集来看，咱们不错发现自然数与自然数的子集组成的团结之间具有不同的基数，假设咱们把自然数与不同的自然数子集建筑一个对应关系，1: M1 2: M2....，采用对角线步伐，咱们老是不错构造出一个新的自然数集，它莫得任何自然数与之对应，咱们这么产生这个新的自然数集：若是i属于Mi，那么摈斥i，不然包含i，容易看到这么产生的一个团结不同于任何的Mi。可见由一切自然数集组成的团结的基数要大于自然数的基数。

本质上康托尔并不是第一个关心到无尽的数量特等性的东谈主，早在17世纪，莱布尼茨就发现偶数和自然数是逐个双应的，正如他所说：对于任何一个数，王人存在一个与之对应的偶数，那就是它的二倍。因此所稀有的数量并不比偶数的数量更多，也就是说举座莫得部分大。可是他得出了这么一个论断：扫数自然数的数量这一主见是不一致的，计齐统共无尽鸠集元素的数量是没特谈理谈理的。可是康托了弃取了另一条路，他承认某些无尽集将与它的一个子集具有相似的元素数量。恰是基于这么一个斗胆的弃取，他才创立了对于无尽的新表面。

当康托尔提议这些不雅点之后，坐窝引来了各方面的抑遏。与弗雷格雷同，东谈主们发现用康托尔的超限数进行不加死字的推招待导致诞妄的成果。比如若是存在一个由扫数基数组成的团结，那么它的基数该是些许呢？它必须比扫数基数王人大，但一个基数又怎么可能比扫数基数王人大呢？其后罗素又指出这么的一个问题：是否存在一个扫数团结的团结？若是存在，那么倘若把对角线步伐应用于它，会出现什么成果？这么咱们会得到一个不同于扫数那些还是领有标签的团结的团结。恰是在筹商这种情况时，罗素发现他阿谁对于由一切不是自身的团结组成的团结的驰名悖论，也就是他向弗雷格传达的阿谁悖论。这里咱们看到，弗雷格和康托尔之间被罗素悖论臆想起来。而对于这个悖论的讨论和想考，则激励了数学史上的第三次危急。

大卫希尔伯特

希尔伯特是20世纪的数学首脑，1900年他在数学家大会上指出的23个问题，其中第二个就是对于算术一致性的问题。即關於一個公理系統相容性的問題，也就是判定一個公理系統內的所命題是互相相容無矛盾的，希爾伯特但愿能以嚴謹的方式來證明任性公理系統內命題的相容性。

希尔伯特纲要所提议的主要问题就是算术一致性问题。为了惩处这个问题，希尔伯特发展出了元数学，一致性诠释将在元数学里面完成。1928年，希尔伯特和他的学生阿克曼出书了一册逻辑讲义，书中提议了对于弗雷格>的基本逻辑(其后被称为一阶逻辑)两个主要问题，一个就是，诠释一阶逻辑的完备性，即任何一个从外部看来有用的公式王人不错只用讲义里提议轨则从系统里面导出。第二个问题以希尔伯特的判定问题而驰名，即对于一个一阶逻辑的公式，若是找到一种步伐，不错在界阐发确有限风光内判定这个公式是有用的。这两个问题分别为哥德尔和图灵惩处，而在惩处第二个问题的历程中，图灵提议了图灵机的主见。

其后在1928年的外洋数学家大会上，希尔伯特又提议一个对于神志系统的问题，这个系统建筑在把一阶逻辑应用于当今被称为皮亚诺算术或者PA的自然数公理系统的基础之上。希尔伯特但愿不错诠释PA是完备的，也就是说任何一个不错在PA中表出的命题或者不错在PA中被诠释为真，或者不错被诠释为假。两年后，这个问题被一个叫哥德尔的年青东谈主惩处了，但谜底却完竣不像希尔伯特料想的那样。

哥德尔完备性定理

希尔伯特在20世纪20年代先容了他的元数学纲要：一致性有待诠释的公理将被包含在一个神志逻辑系统之内，而诠释只是是有限数方针符号的一种成列汉典。当希尔伯特运行想考希尔伯特纲要时，希尔伯特的学生阿克曼和冯诺依曼似乎正执政着用有限性步伐诠释PA的一致性的标的大步迈进。他们二东谈主王人还是为PA的一个有限的子系统找到了这么的诠释，生效似乎计日而待。

这么哥德尔运行试图将算术一致性收复为PA的一致性，关联词就是在这么的奋发中失败了。哥德尔运行想考这些问题时，他再行想考了从外部而不是从里面测验一个系统的谈理。从外部看，这些系统包含着符号串之间的关系。从里面看，这些系统能够抒发对于不同数学对象的命题。哥德尔通过给符号串用自然数编码，将外部带到了里面。

哥德尔发现有在这么的命题，它们从系统外部看是真命题，但无法在系统里面得到诠释。于是他得出了一个不凡论断：一种特谈理谈理的数学真谛的不雅念不仅是存在的，而且其边界还超出了任何给定的神志系统的诠释才调。在1931年，他发表的论文及相干系统的神志不可判定命题>>中，他弃取对神志系统PM给出了他的成果，从而阐发即使强逻辑系统也不可能把沿路数学真谛包含在内。

在哥德尔的诠释中，关键的一步在于他诠释了：一个自然数作为PM中可证命题的一个代码，这一性质自身不错在PM中暗示出来。笔据这一事实，哥德尔不错在PM中构造出一些命题，这些命题不错被看作念抒发了这么一个断言，即某些命题在PM中是不可证的。也就是说他不错构造出一个命题A，该命题经译码后不错断言某一命题B在PM中是不可证的。当今，在莫得获知密码的东谈主看来，命题A不外是一串符号汉典，可是通过代码，深重性就消散了：A暗示这么一个命题，即某个符号串B暗示在PM中一个不可证的命题。A和B常常是不同的命题，哥德尔问，它们是否有可能是相似的呢？事实上它们不错是相似的，哥德尔不错利用对角线步伐诠释这个论断。

哄骗这些技巧，咱们不错使被断言为不可证的命题和作念出这一断言的命题是并吞个命题。换句话说哥德尔发现了若是获取这么一个不凡的命题，咱们将它称以外U，具有如下性质：

U说某个特等命题在PM中不可证。

阿谁特等的命题就是U自身。

因此，U说"U在PM中不可证"

若是咱们承认PM中诠释的任何命题王人是确实，那么咱们发现U是确实，但它在PM中不可证。

U是确实。假设它是假的，那么它表述的内容就是假的，因此它就是不是不可证的，而一定是可证的，从而是确实，这与运行假设U是假的矛盾，是以它一定是确实。因为它是确实，是以它表述的内容为真，是以它在PM中不可证。

咱们把U称为不可判定命题，自然这种不可判断性只与系统里面的可证性，从咱们外部的不雅点来看U是确实。

另一方面，在PM里面，咱们不错诠释：若是PM是一致的，那么U。因此恰是PM是一致的这一个假设，才使U在PM里面得不到诠释。既然咱们知谈U在PM里面是不可证的，咱们就必须得出结阐发，PM的一致性在PM中不可证。而希尔伯特的主要方针就在于：用于被觉得组成PM的一个相等有限的子集的有限性步伐来诠释像PM这么的系统的一致性。关联词哥德尔诠释了，即使就PM的沿路才调而言，它也不及以诠释自身的一致性。于是希尔伯特纲要走到了绝顶。

图灵和图灵机

在哥德尓1930年的博士论文中诠释了弗雷格的轨则是完备的，这么就报酬了希尔伯特1928年提议的第一个问题。而第二个问题即判定问题，在哥德尔的责任发表之后，东谈主们很难遐想存在这么的判定算法，于是阿兰图灵运行想考若是诠释这么的算法是不存在的。

图灵选择了这么的一条谈路，他当先分析了东谈主的筹画历程。通过丢掉非实质的细节，将这些筹画行径局限在少数几种极为浅薄的基本操作上。然后图灵阐发东谈主不错被一个能够扩充这些基本操作的机器所替代。然后只消诠释只是扩充那些基本操作的机器不可能判定一个给定的论断是否不错用弗雷格的轨则从给定的前提中导出，这么他就能够下结阐发，判定问题的算法是不存在的。

作为副居品，他对筹画历程的分析，产生了通用筹画机的一个数学模子。

他不雅察到：在筹画的每一个阶段，独一少数符号受到了选藏。每一个阶段所选择的行径只是取决于受到选藏的那些符号以及现时的心灵气象。

然后他作念出了如下玄虚：筹画通过在一条被远离红方格的纸带上写下符号来进行。扩充筹画的东谈主在每一步王人只选藏其中一个方格的符号。她的下一步将只是取决于这个符号和她的心灵气象。她的下一步是这么的：她在现时选藏的方格里写下一个符号，然后将珍见解转向它左边或者右边的相邻符号。

当今不错很容易看出，作念这项责任的东谈主不错用一个机器替代，纸带在机器上往来迁徙。关键之处在于图灵对于筹画主见的分析，通过某种算法例范可筹画的任何东西王人不错通过一台图灵机来筹画。因此若是咱们不错诠释某些任务无法用图灵机完成，那么咱们就不错说莫得任何算法不错完成这项任务。这就是图灵诠释判定问题不存在算法的步伐。

本质上一台图灵机不错用这么的一个五元组来暗示：当机器处于气象R，扫视纸带上的符号a时，它将用b来代替a，向右迁徙一个方格，然后转到气象S。而一个具体的算法便不错由这些五元组暗示的气象颐养的团结组成的图灵机来暗示出来。R a:b -> S 或者R a:b

图灵将对角线步伐应用于这种情况，得到了图灵机不可惩处的问题，由此推出了判定问题的不可解性。与哥德尓雷同，图灵采用了对角线步伐也对图灵机通过自然数进行了编码。

图灵机自身不错是自然数编码暗示，这么它也作为自身的输入。本质上有些输入会使图灵机住部属来，另一些则不会。这么一台图灵机就具有一些停机团结。若是咱们筹商把一台图灵机的停机团结组成了一个包裹，况且觉得那台机器的码数就是这个包裹的标签。对角线步伐允许咱们构造出一个与图灵机的任何停机团结王人不同的自然数团结，咱们称之为D。步伐是这么的，咱们筹商把图灵机的编码作为自身的输入，若是它的编码数不属于自身的停机团结，那么咱们就把它加入D。而团结D则不是任何图灵机的停机团结。

然后筹商这么一个问题：

找到一种算法，判定一个给定的自然数是否属于团结D。

这就是一个不可解问题的例子。当先若是存在这么的一个算法，咱们就能找到这么的一个图灵机，可是我不错矫正一下这个图灵机，把以下两个五元组加入到这个图灵机：F 0:口-> F 和 F 口:口-> F。对于这个新的改进的图灵机来说，若是输入的数属于D那么那么机器就会像曩昔一样运转，并输出1而告终，若是输入的数不属于D，那这台机器将恒久向右迁徙。这么咱们就找到了一台图灵机它的停机团结刚好就是D。于是与咱们的对角线步伐矛盾。是以并不存在这么的一个算法。由此可知判断问题在算法上是不可解的。

为了考证我方责任的有用性，图灵又提议了通用机模子，通用机包含了图灵机代码以及待处理的数据。而这刚好对应着咱们今天的机器，轨范与数据的主见。也为存储轨范筹画机提供了一个模子。恰是图灵在诠释判定问题的不可解性是，对筹画主见的分析以及对通用机的发现促使了筹画机的产生。

1945年图灵又发表了他那篇驰名的ACE(自动筹画机)文牍。这是对筹画机的一次完满的态状，一直到逻辑电路图。也就是在这时冯诺依曼提议了他驰名的"对于EDVAC的文牍草案"，它本质上主张将要建造的EDVAC作为图通畅用机的一个物理模子杀青出来。在这个文牍里，提议了存储轨范的主见，也就是沿用于今的冯诺依曼结构，本质上它的立异性不在于存储轨范而是通用性，存储轨范只是达到这一方针的一种手艺。

1950年，图灵又发表了他的经典论文，筹画机与智能，提议了驰名的图灵测试来测试筹画机是否具有智能。1954年6月7日，图灵咬了一个浸过氰化物的苹果东京热qvod，末端了我方的人命。而他的通用机想想却延续到今天。